|
Страница 4 из 5 Теорию n-руких бандитов можно использовать для обоснования приемлемости стратегии отбора в генетических алгоритмах (см. главу 4). Если в задаче с n-руким бандитом каждая рукоятка рассматривается как возможная строка генов, а вкладывание монеты для подтягивания одной рукоятки — как воспроизведение этих генов, то генетические алгоритмы должны обеспечить оптимальное вложение монет в игорный автомат с учетом соответствующего множества предположений о независимости. Хотя задачи с n-рукими бандитами чрезвычайно трудно поддаются точному решению для получения оптимального метода исследования среды, тем не менее возможно предложить приемлемую схему, которая в конечном итоге приводит к оптимальному поведению со стороны агента. Формально любая такая схема должна быть жадной в пределе бесконечного исследования; это свойство сокращенно обозначается как GLIE (Greedy in the Limit of Infinite Exploration). Схема GLIE должна предусматривать опробование каждого действия в каждом состоянии путем осуществления неограниченного количества попыток такого действия для предотвращения появления конечной вероятности того, что будет пропущено какое-то оптимальное действие из-за крайне неудачного стечения обстоятельств. Агент ADP, в котором используется такая схема, должен в конечном итоге определить с помощью обучения истинную модель среды. Кроме того, схема GLIE должна в конечном итоге стать жадной, для того чтобы действия агента стали оптимальными по отношению к определенной с помощью обучения (и поэтому истинной) модели. Предложено несколько схем GLIE; в одной из простейших из этих схем предусматривается, что агент должен в течение 1/t части времени выбирать случайное действие, а в течение остального времени придерживаться жадной стратегии. Хотя такая схема в конечном итоге сходится к оптимальной стратегии, весь этот процесс может оказаться чрезвычайно замедленным. Более обоснованный подход предусматривает присваивание определенных весов тем действиям, которые агент не опробовал очень часто, стараясь вместе с тем избегать действий, которые считаются имеющими низкую полезность. Такой подход может быть реализован путем модификации уравнения ограничения 21.4 таким образом, чтобы в нем присваивалась более высокая оценка полезности относительно мало исследованным парам "состояние—действие". По сути это сводится к определению оптимистического распределения априорных вероятностей по возможным вариантам среды и вынуждает агента на первых порах вести себя так, как если бы повсеместно были разбросаны замечательные вознаграждения. Допустим, что для обозначения оптимистической оценки полезности состояния s (т.е. ожидаемого будущего вознаграждения) используется запись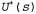 , и предположим, что N(a, s) — количество попыток опробования действия а в состоянии s. Предположим также, что в обучающемся агенте ADP используется метод итерации по значениям; в таком случае необходимо переписать уравнение обновления (т.е. уравнение 17.6), чтобы включить в него оптимистическую оценку. Именно такая цель достигается с помощью следующего уравнения: , и предположим, что N(a, s) — количество попыток опробования действия а в состоянии s. Предположим также, что в обучающемся агенте ADP используется метод итерации по значениям; в таком случае необходимо переписать уравнение обновления (т.е. уравнение 17.6), чтобы включить в него оптимистическую оценку. Именно такая цель достигается с помощью следующего уравнения: 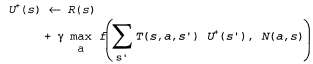 (21.5) (21.5)
|