Как было показано выше, правило Байеса может применяться для получения ответов на вероятностные запросы, в которых учтено условие, составляющее одно из свидетельств, например неподвижная шея. В частности, было показано, что вероятностная информация часто доступна в форме Ρ (effect | cause) (где effect — результат, a cause— причина). А что произойдет, если свидетельств два или больше? Например, какой вывод может сделать зубной врач, если его стальной инструмент захватил больной зуб пациента, причинив еще большие страдания? Если известно полное совместное распределение (табл. 13.2), можно сразу же прочитать ответ: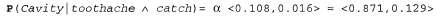

Но нам уже известно, что такой подход не масштабируется на большее количество переменных.

Тогда можно попытаться воспользоваться правилом Байеса для переформулировки этой задачи:

(13.12)

Для того чтобы можно было найти ответ запрос в такой формулировке, необходимо знать условные вероятности конъюнкции toothache л catch для каждого значения Cavity. Такая задача может быть осуществима, если речь идет только о двух переменных свидетельства, но этот подход снова становится источником затруднений при его применении в больших масштабах. Если имеется n возможных переменных свидетельства (рентгеновское обследование, диета, гигиена полости рта и т.д.), то количество возможных комбинаций наблюдаемых значений, для которых необходимо будет знать условные вероятности, составит. С таким же успехом можно было бы снова вернуться к использованию полного совместного распределения. Именно по этой причине исследователи после первых попыток отказались от применения теории вероятностей и обратились к приближенным методам комбинирования свидетельств, в которых требуется использовать меньше чисел для получения ответов, хотя сами эти ответы не всегда бывают правильными.