|
Страница 3 из 3 Обратите внимание на то, что это утверждение немного строже по сравнению с уравнением 13.13, в котором сформулировано утверждение о независимости только для конкретных значений Toothache и Catch. А при использовании свойства абсолютной независимости, сформулированного в уравнении 13.8, могут также применяться следующие эквивалентные формы: 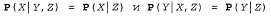
В разделе 13.5 показано, что утверждения с описанием свойств абсолютной независимости позволяют выполнять декомпозицию полного совместного распределения на гораздо более мелкие распределения. Как оказалось, аналогичную декомпозицию позволяют выполнять утверждения об условной независимости. Например, с помощью утверждения, приведенного в уравнении 13.14, декомпозицию можно вывести следующим образом: 
Таким образом, первоначальная крупная таблица декомпонована на три меньшие таблицы. В исходной таблице было семь независимых чисел (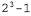 , поскольку эти числа должны в сумме составлять 1). Меньшие таблицы содержат пять независимых чисел , поскольку эти числа должны в сумме составлять 1). Меньшие таблицы содержат пять независимых чисел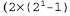 для каждого распределения условных вероятностей и для каждого распределения условных вероятностей и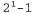 для распределения априорной вероятности Cavi ty). Такое достижение на первый взгляд может показаться не очень значительным, но дело в том, что для η симптомов, являющихся условно независимыми, если дана вероятность Cavity, размер представления растет как 0{п), а не для распределения априорной вероятности Cavi ty). Такое достижение на первый взгляд может показаться не очень значительным, но дело в том, что для η симптомов, являющихся условно независимыми, если дана вероятность Cavity, размер представления растет как 0{п), а не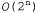 . Таким образом, z утверждения об условной независимости могут обеспечивать масштабирование вероятностных систем; более того, такие утверждения могут быть подкреплены данными намного проще по сравнению с утверждениями об абсолютной независимости. С концептуальной точки зрения переменная Cavity разделяет переменные Toothache и Catch, поскольку наличие дупла является прямой причиной и зубной боли, и наложения инструмента на зуб. Разработка методов декомпозиции крупных вероятностных областей определения на слабо связанные подмножества с помощью свойства условной независимости стало одним из наиболее важных достижений в новейшей истории искусственного интеллекта. . Таким образом, z утверждения об условной независимости могут обеспечивать масштабирование вероятностных систем; более того, такие утверждения могут быть подкреплены данными намного проще по сравнению с утверждениями об абсолютной независимости. С концептуальной точки зрения переменная Cavity разделяет переменные Toothache и Catch, поскольку наличие дупла является прямой причиной и зубной боли, и наложения инструмента на зуб. Разработка методов декомпозиции крупных вероятностных областей определения на слабо связанные подмножества с помощью свойства условной независимости стало одним из наиболее важных достижений в новейшей истории искусственного интеллекта. Приведенный выше пример из области стоматологии может служить проявлением часто встречающейся ситуации, в которой одна причина непосредственно влияет на целый ряд результатов, причем все эти результаты являются условно независимыми, если дана эта причина. Полное совместное распределение может быть записано следующим образом: 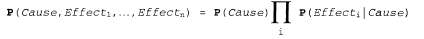
Указанное распределение вероятностей называется наивной байесовской моделью. Такая модель называется "наивной", поскольку часто используется (как упрощающее допущение) в тех случаях, когда переменные "результата" не являются условно независимыми, если дана переменная причины. (Наивную байесовскую модель иногда называют байесовским классификатором, а это не совсем корректное применение термина побудило настоящих специалистов в области байесовских моделей называть ее не наивной, а идиотской байесовской моделью.) На практике наивные байесовские системы могут действовать удивительно успешно, даже если предположение о независимости не является истинным. В главе 20 описаны методы изучения наивных байесовских распределений поданным наблюдений.
<< В начало < Предыдущая 1 2 3 Следующая > В конец >>
|