|
Страница 2 из 3 Вместо того чтобы следовать по такому пути, мы должны найти некоторые дополнительные утверждения о рассматриваемой проблемной области, которые позволят упростить применяемые выражения. Понятие независимости, приведенное в разделе 13.5, дает ключ к этому решению, но требует уточнения. Было бы прекрасно, если бы переменные Toothache и Catch были независимыми, но они таковыми не являются: если зубной врач захватывает зуб своим инструментом, то он делает это, вероятно, потому, что в этом зубе есть дупло, а это действие, вероятно, в свою очередь вызывает боль. Но эти переменные независимы, если речь идет о наличии или отсутствии дупла. Причиной каждого из соответствующих действий было дупло, но ни одно из них не оказывает непосредственного влияния на другое: зубная боль зависит от состояния нервов в зубе, а точность наложения инструмента зависит от навыков зубного врача, к которым зубная боль не имеет отношения. Математически это свойство записывается следующим образом: 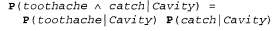 (13.13) (13.13)
В данном уравнении выражена условная независимость переменных toothache и catch, если дана вероятность Cavity. Соответствующее выражение можно вставить в уравнение 13.12 для определения вероятности наличия дупла: 
Теперь требования к наличию информации становятся такими же, как и при вероятностном выводе с использованием каждого свидетельства отдельно: необходимо знать априорную вероятность Ρ (Cavi ty) для переменной запроса и условную вероятность каждого результата, если дана его причина. Общее определение условной независимости двух переменных X и Y, если дана третья переменная Z, выражается следующей формулой: 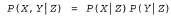
Например, в проблемной области стоматологии представляется вполне резонным применение утверждения об условной независимости переменных Toothache и Catch, если дана вероятность Cavi ty. 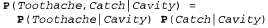 (13.14) (13.14)
|