|
Из этих основных аксиом можно вывести целый ряд полезных фактов. Например, знакомое правило отрицания следует из подстановки вместо b в аксиому 3, что приводит к получению следующего выражения: вместо b в аксиому 3, что приводит к получению следующего выражения: 
Третья строка этого логического вывода сама является полезным фактом и может быть распространена с данного булева случая на общий дискретный случай. Допустим, что дискретная переменная D имеет область определения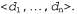 Тогда можно легко показать, что справедлива следующая формула: Тогда можно легко показать, что справедлива следующая формула: 
Это означает, что любое вероятностное распределение по одной переменной должно в сумме6 составлять 1. Справедливо также утверждение, что любое совместное распределение вероятностей по любому множеству переменных должно в сумме составлять 1; в этом можно убедиться, создав одну мегапеременную, областью определения которой является перекрестное произведение областей определения первоначальных переменных. Напомним, что любое высказывание а эквивалентно дизъюнкции всех атомарных событий, в которых а является истинным; назовем эту дизъюнкцию множеством событий е (а). Напомним также, что атомарные события являются взаимно исключающими, поэтому вероятность любой конъюнкции атомарных событий равна нулю, согласно аксиоме 2. Таким образом, из аксиомы 3 можно вывести следующее простое соотношение: вероятность любого высказывания равна сумме вероятностей атомарных событий, в которых оно является истинным; т.е. вывести такое уравнение: 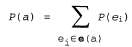 (13.2) (13.2)
Это уравнение предоставляет простой метод вычисления вероятности любого высказывания при наличии полного совместного распределения, которое задает вероятности всех атомарных событий (см. раздел 13.4.) В следующих разделах будут выведены дополнительные правила для манипулирования вероятностями. Но вначале исследуем теоретические основы самих этих аксиом.
|