|
Страница 3 из 3 Теперь необходимо объяснить, как вычисляются эти новые конфликтные множества. Применяемый для этого метод фактически очень прост. "Окончательная" неудача в какой-то ветви поиска всегда возникает из-за того, что область определения некоторой переменной становится пустой; эта переменная имеет типичное конфликтное множество. В данном примере неудача возникает при присваивании значения переменной SA, а ее конфликтным множеством является (скажем) 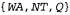 . Выполняется обратный переход к переменной Q, и эта переменная поглощает конфликтное множество, полученное от SA (безусловно, после исключения из него самой переменной Q), объединяя его со своим собственным прямым конфликтным множеством, представляющим собой {NT,NSW}, новым конфликтным множеством становится {WA,NT,NSW}. Это означает, что, продолжая поиск от Q, нельзя найти решение при наличии ранее выполненного присваивания переменным {WA,NT, NSW). Поэтому обратный переход выполняется к переменной NT, присваивание значения которой выполнено последним по времени по сравнению с другими этими переменными. Переменная NT поглощает множество . Выполняется обратный переход к переменной Q, и эта переменная поглощает конфликтное множество, полученное от SA (безусловно, после исключения из него самой переменной Q), объединяя его со своим собственным прямым конфликтным множеством, представляющим собой {NT,NSW}, новым конфликтным множеством становится {WA,NT,NSW}. Это означает, что, продолжая поиск от Q, нельзя найти решение при наличии ранее выполненного присваивания переменным {WA,NT, NSW). Поэтому обратный переход выполняется к переменной NT, присваивание значения которой выполнено последним по времени по сравнению с другими этими переменными. Переменная NT поглощает множество 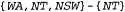 , , объединяя его со своим собственным прямым конфликтным множеством IWA}, что приводит к получению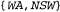 (как было указано в предыдущем абзаце). Теперь алгоритм осуществляет обратный переход к NSW, как и предполагалось. Подведем итог: допустим, что xj — текущая переменная, а (как было указано в предыдущем абзаце). Теперь алгоритм осуществляет обратный переход к NSW, как и предполагалось. Подведем итог: допустим, что xj — текущая переменная, а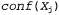 — ее конфликтное множество. Если все попытки присваивания каждого возможного значения переменной xj оканчиваются неудачей, то необходимо выполнить возврат к переменной xi с последним по времени присвоенным значением во множестве — ее конфликтное множество. Если все попытки присваивания каждого возможного значения переменной xj оканчиваются неудачей, то необходимо выполнить возврат к переменной xi с последним по времени присвоенным значением во множестве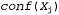 и установить: и установить: 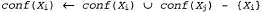
Обратный переход, управляемый конфликтами, позволяет вернуться в правильную точку дерева поиска, но не предотвращает возможности возникновения таких же ошибок в другой ветви того же дерева. Метод определения ограничений с помощью обучения (constraint learning) по сути представляет собой метод модификации задачи CSP путем добавления нового ограничения, выдвинутого на основе логического анализа этих конфликтов.
<< В начало < Предыдущая 1 2 3 Следующая > В конец >>
|