Любой алгоритм детерминированного контролируемого обучения получает в качестве исходной информации правильные значения неизвестной функции, соответствующие конкретным входным данным, и должен предпринять попытку восстановить эту неизвестную функцию или сформировать какую-то другую функцию, близкую к ней. Более формально можно определить, что пример представляет собой пару (х, f (х) ), где х— входное, a f (x) — выходное значение функции, применяемой к х. Основная задача чисто индуктивного логического вывода (или просто индукции) указана ниже.

На основании совокупности примеров входных и выходных данных функции f получить функцию h, которая аппроксимирует f.

Функция h называется гипотезой. С концептуальной точки зрения та причина, по которой задача обучения является трудной, состоит в том, что обычно нелегко определить, действительно ли какая-то конкретная функция h является хорошей аппроксимацией для f. Качественная гипотеза должна обеспечивать приемлемое обобщение, т.е. должна правильно предсказывать появление еще не полученных примеров. В этом состоит фундаментальная проблема индукции. Эта проблема изучалась в течение многих столетий; в разделе 18.5 приведено ее частичное решение.

На рис. 18.1 приведен известный пример: подгонка функции от одной переменной к некоторым точкам из набора данных. Примеры представляют собой пары (х, f(x) ), где и χ и f(x) — действительные числа. Выберем в качестве пространства гипотез Η (множества гипотез, которые мы будем рассматривать в качестве потенциально приемлемых) множество полиномов, имеющих степень не больше k, таких как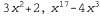и т.д. На рис. 18.1, а показаны данные, которые соответствуют некоторой прямой (полиному первой степени). Эта прямая называется совместимой с гипотезой, поскольку она согласуется со всеми данными. На рис. 18.1,5 показан полином более высокой степени, который также согласуется с этими данными. Данный случай может служить иллюстрацией к наиболее важной проблеме в индуктивном обучении: как осуществлять выбор среди многочисленных согласованных гипотез? Ответ состоит в использовании принципа бритвы Оккама, согласно которому предпочтение следует отдавать наиболее простой гипотезе, согласующейся с данными. Интуитивно ясно, что такой подход имеет смысл, поскольку гипотезы не позволяют извлекать из данных какую-либо информацию, если они не проще самих данных. Определить, какая гипотеза проще, а какая сложнее, обычно нелегко, но, по-видимому, вполне резонным является утверждение, что полином первой степени проще по сравнению с полиномом двенадцатой степени.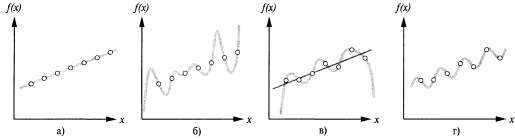

Рис. 18.1. Типичные задачи обучения: пример пар (x,f(x)) и совместимой линейной гипотезы (а); совместимая гипотеза для того же набора данных в виде полинома седьмой степени (б); другой набор данных, который точно соответствует полиному шестой степени или приблизительно соответствует прямой линии (в); простая синусоидальная функция, которая точно соответствует тому же набору данных (г)