Рассмотрим эту идею немного более конкретно. Функции оценки чаще всего действуют по принципу вычисления различных характеристик данного состояния, например, в шахматах одной из таких характеристик является количество пешек, принадлежащих каждой из сторон. Эти характеристики, вместе взятые, определяют различные категории, или классы эквивалентности состояний: состояния из каждой категории имеют одни и те же значения для всех своих характеристик. Вообще говоря, любая конкретная категория включает некоторые состояния, которые ведут к победе, к ничьей или поражению. Функция оценки не позволяет определить, какими являются те или иные состояния, но способна вернуть единственное значение, которое отражает процентную долю этих состояний в каждом результате. Например, предположим, полученный опыт показывает, что 72% состояний, встретившихся в данной категории, ведут к победе (полезность +1); 20% — к поражению (-1) и 8% к ничьей (0). В таком случае приемлемой оценкой для состояний этой категории становится взвешенное среднее, или дожидаемое значение: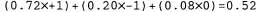 В принципе, ожидаемое значение можно определить для каждой категории, получив в итоге функцию оценки, применимую для любого состояния. Как и в случае терминальных состояний, функция оценки не обязана возвращать фактические ожидаемые значения, при условии, что упорядочение состояний остается тем же самым.

На практике для проведения анализа такого рода требуется учитывать слишком много категорий и поэтому накопить слишком много опыта, чтобы можно было оценить все вероятности выигрыша. Вместо этого в большинстве функций оценки вычисляются отдельные представленные в числовом виде значения вклада, зависящего от каждой характеристики, после чего эти значения комбинируются для поиска суммарного значения. Например, в учебниках по шахматам для начинающих можно найти приближенные оценки стоимости материала для каждой фигуры: например, такие, что пешка имеет стоимость 1, конь или слон— 3, ладья— 5, а ферзь— 9. Другие характеристики, такие как "хорошая пешечная структура" и "безопасность короля", могут оцениваться как равные, скажем, половине стоимости пешки. После этого стоимости таких характеристик просто складываются для получения оценки позиции. Надежное преимущество, эквивалентное стоимости пешки, расценивается как значительная вероятность выигрыша, а надежное преимущество в три пешки должно почти наверняка обеспечить победу, как показано на рис. 6.6, а. В математике функция оценки такого типа называется взвешенной линейной функцией, поскольку она может быть представлена следующим образом: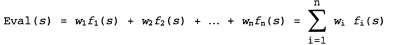

где каждый коэффициент wi представляет собой вес, а каждая функция fi оценивает некоторую характеристику позиции. В шахматах функция fi. может определять количество на доске фигур каждого вида, а коэффициент wi — оценивать стоимости этих фигур (1 за пешку, 3 за слона и т.д.).