Формально свойство высказывания, позволяющее свободно подставлять любой терм вместо равного терма, называется ссылочной прозрачностью (referential transparency). В логике первого порядка свойством ссылочной прозрачности обладает каждое отношение. Но нам было бы желательно иметь возможность определять Believes (и другие пропозициональные позиции) как отношения, второй параметр которых является ссылочно непрозрачным (opaque), т.е. таким, чтобы без изменения смысла нельзя было бы подставить равный терм вместо второго параметра.

Существуют два способа достижения этой цели. Первый из них состоит в использовании другой формы логики, называемой модальной логикой (modal logic), в которой такие пропозициональные позиции, как Believes и Knows, становятся модальными операторами, обладающими свойством ссылочной непрозрачности. Этот подход рассматривается в разделе с историческими заметками. Второй подход, который будет применяться в данной главе, состоит в эффективном обеспечении непрозрачности в рамках ссылочно прозрачного языка с использованием синтаксической теории мыслимых объектов. Это означает, что мыслимые объекты представляются константами — строками. Результатом становится грубая модель базы знаний агента, которая представлена как состоящая из строк, соответствующих высказываниям, в истинности которых убежден агент. Строка — это сложный терм, обозначающий список символов, поэтому событие Flies (Clark) может быть представлено в виде списка символов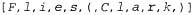, которые мы будем сокращенно записывать в виде строки, заключенной в кавычки, "Flies(Clark) ". Эта синтаксическая теория включает аксиому об уникальности строк, в которой утверждается, что строки являются идентичными тогда и только тогда, когда они состоят из идентичных символов в одинаковой последовательности. Таким образом, даже если Clark= Superman, мы все равно имеем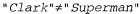

Теперь достаточно лишь предусмотреть синтаксис, семантику и теорию доказательства для языка представления строк, точно так же, как это было сделано в главе 7. Различие состоит в том, что необходимо определить все эти компоненты в логике первого порядка. Начнем с определения Den (сокращение от denotatum — денотат, или обозначаемое) как функции, которая отображает некоторую строку на обозначаемый ею объект, и Name как функции, которая отображает объект на строку, представляющую собой имя константы, обозначающей этот объект. Например, денотатом строки " Clark" и строки " Superman" является объект, на который ссылается константный символ ManOf Steel (Человек из стали), а именем этого объекта в базе знаний может быть " Superman", " Clark" или какая-то другая константа, например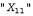: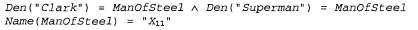