|
Страница 2 из 4 Кроме того, целесообразно определить составные объекты, имеющие различимые части, но не имеющие конкретной структуры. Например, может потребоваться сформулировать утверждение: "Яблоки в этой сумке весят два килограмма". Может возникнуть соблазн приписать этот вес множеству яблок в сумке, но это было бы ошибкой, поскольку множество — это абстрактное математическое понятие, которое имеет элементы, но не имеет веса. Вместо этого необходимо ввести новое понятие, которое мы будем именовать совокупностью (BunchOf). Например, если три яблока обозначены как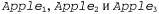 , то выражение , то выражение 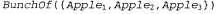 обозначает составной объект, частями (а не элементами) которого являются три яблока. Затем эта совокупность может использоваться как обычный, хотя и не структурированный объект. Обратите внимание на то, что BunchOf ({x}) = x. Кроме того, BunchOf (Apples) — это составной объект, состоящий из всех яблок, но его не следует путать с объектом Apples — категорией или множеством всех яблок. обозначает составной объект, частями (а не элементами) которого являются три яблока. Затем эта совокупность может использоваться как обычный, хотя и не структурированный объект. Обратите внимание на то, что BunchOf ({x}) = x. Кроме того, BunchOf (Apples) — это составной объект, состоящий из всех яблок, но его не следует путать с объектом Apples — категорией или множеством всех яблок. Определим понятие BunchOf в терминах отношения PartOf. Очевидно, что каждый элемент множества s — это часть объекта BunchOf is): 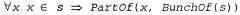
Более того, BunchOf(s) — это наименьший объект, удовлетворяющий данному условию. Иными словами, BunchOf(s) должен быть частью любого объекта, который включает все элементы множества s в качестве части: 
Эти аксиомы представляют собой пример общего метода, называемого логической минимизацией, с помощью которого любой объект может быть определен как наименьший объект, удовлетворяющий определенным условиям.
|