В операциях суммирования первым множителем является модель перехода, а вторым — распределение вероятностей для текущего состояния. Поэтому получена требуемая рекурсивная формулировка. Отфильтрованная оценка может рассматриваться как "сообщение", которое распространяется в прямом направлении вдоль последовательности состояний, будучи модифицируемым при каждом переходе и обновляемым при получении каждого нового результата наблюдения. Этот процесс можно представить следующим образом: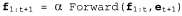

где функция Forward реализует обновление, описанное в уравнении 15.3.

Если все переменные состояния являются дискретными, то затраты времени на каждое обновление остаются постоянными (т.е. независимыми от t) и потребность в пространстве также остается постоянной. (Соответствующие постоянные показатели временной и пространственной сложности, безусловно, зависят от размера пространства состояний и от конкретного типа используемой временной модели.) Требования ко времени и пространству для обновления должны быть постоянными, если агент с ограниченной памятью обязан следить за распределением вероятностей для текущего состояния на протяжении неограниченной последовательности наблюдений.

Проиллюстрируем процесс фильтрации, состоящий из двух этапов, на простом примере с зонтиком (см. рис. 15.2). Предполагается, что охранник обладает с определенной степенью уверенности сведениями о распределении априорных вероятностей дождя в день 0, непосредственно до того, как началась данная последовательность наблюдений. Предположим, что данным распределением является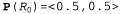. Теперь обработаем результаты двух наблюдений, как показано ниже.

• В день 1 директор пришел с зонтиком, поэтому и1= true. Результаты предсказания перехода от t=0 к t=l состоят в следующем:

а их обновление с помощью свидетельства, полученного для t = 1, является таковым:

• В день 2 директор также пришел с зонтиком, поэтому U2=true. Результаты предсказания перехода от t=l к t=2 являются следующими: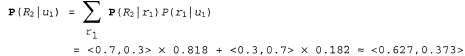

а обновление их с помощью свидетельства для t=2 позволяет получить следующее: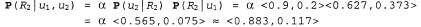

Интуитивно ясно, что вероятность дождя от дня 1 ко дню 2 повышается, поскольку дождь продолжается. В упр. 15.2, а предлагается исследовать такую тенденцию дальше.