Минимальное множественное покрытие цели {А, В, С] задается действиями {Χ, Υ], поэтому эвристика множественного покрытия возвращает стоимость 2. Такая оценка лучше по сравнению с предположением о независимости подцелей, которое позволяет получить эвристическое значение 3. Остается непреодоленной лишь одна небольшая неприятная особенность: задача поиска множественного покрытия является NP-трудной. Простой жадный алгоритм поиска множественного покрытия гарантирует возвращение значения, которое находится в пределах коэффициента logn от истинного минимального значения, где п— количество литералов в цели, но обычно на практике данный алгоритм действует намного лучше по сравнению с этой оценкой. К сожалению, жадный алгоритм не обеспечивает гарантий достижимости для такой эвристики.

Существует также возможность создавать ослабленные задачи, удаляя отрицательные результаты без удаления предусловий. Таким образом, если некоторое действие в первоначальной задаче имеет результат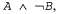то в ослабленной задаче будет иметь результат А. Это означает, что не нужно беспокоиться об отрицательных взаимодействиях субпланов, поскольку ни одно действие не способно удалить литералы, достигнутые другим действием. Стоимость решения полученной в конечном итоге ослабленной задачи задает то, что принято называть эвристикой с пустым списком удаления. Эта эвристика является весьма точной, но для ее вычисления требуется действительно выполнить некоторый (простой) алгоритм планирования. Тем не менее на практике поиск в условиях ослабленной задачи часто происходит достаточно быстро для того, чтобы имело смысл применение этой оценки стоимости.

Описанные здесь эвристики могут использоваться либо в прогрессивном, либо в регрессивном направлении. Ко времени написания данной книги первые места в рейтинге эффективности занимали прогрессивные планировщики, в которых применялась эвристика с пустым списком удаления. Такая ситуация вполне может измениться в результате исследования новых эвристик и новых методов поиска. Поскольку задачи планирования являются экспоненциально трудными, ни один алгоритм не может быть достаточно эффективным для решения всех задач, но с использованием эвристических методов, описанных в этой главе, могут быть решены многие практические задачи, и таких задач стало гораздо больше по сравнению с теми, которые были решаемыми всего лишь несколько лет тому назад.