Листинг 4.1. Алгоритм рекурсивного поиска по первому наилучшему совпадению

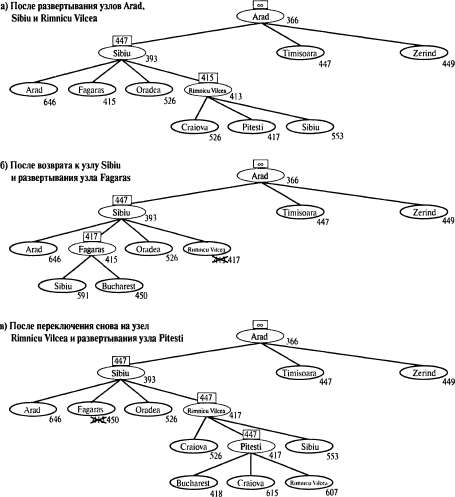
Рис. 4.4. Этапы поиска кратчайшего маршрута в Бухарест с помощью алгоритма RBFS. Значение f-предела для каждого рекурсивного вызова показано над каждым текущим узлом: путь через узел RimnicuVilcea, который следует до текущего наилучшего листового узла (Pitesti,), имеет значение, худшее по сравнению с наилучшим альтернативным путем (Fagaras,) (а);рекурсия продолжается и значение наилучшего листового узла забытого поддерева (417) резервируется в узле Rimni cuVi l cea; затем развертывается узел Fagaras, в результате чего обнаруживается наилучшее значение листового узла у равное 450 (б); рекурсия продолжается и значение наилучшего листового узла забытого поддерева (450) резервируется в узле Fagaras; затем развертывается узел Rimni cuVi lcea; на этот раз развертывание продолжается в сторону Бухареста, поскольку наилучший альтернативный путь (через узел Timisoara стоит, по меньшей мере, 447(e)

Алгоритм RBFS является немного более эффективным по сравнению с IDA*, но все еще страдает от недостатка, связанного со слишком частым повторным формированием узлов. В примере, приведенном на рис. 4.4, алгоритм RBFS вначале следует по пути через узел RimnicuVilcea, затем "меняет решение" и пытается пройти через узел Fagaras, после этого снова возвращается к отвергнутому ранее решению. Такие смены решения происходят в связи с тем, что при каждом развертывании текущего наилучшего пути велика вероятность того, что его f-значение увеличится, поскольку функция h обычно становится менее оптимистической по мере того, как происходит развертывание узлов, более близких к цели. После того как возникает такая ситуация, особенно в больших пространствах поиска, путь, который был вторым после наилучшего, может сам стать наилучшим путем, поэтому в алгоритме поиска приходится выполнять возврат, чтобы проследовать по нему. Каждое изменение решения соответствует одной итерации алгоритма IDA* и может потребовать многих повторных развертываний забытых узлов для воссоздания наилучшего пути и развертывания пути еще на один узел.