|
В этом разделе будут рассматриваться эвристические функции для задачи игры в восемь, что позволяет лучше продемонстрировать характерные особенности всех эвристических функций в целом. Головоломка "игра в восемь" была одной из первых задач эвристического поиска. Как было указано в разделе 3.2, в ходе решения этой головоломки требуется передвигать фишки по горизонтали или по вертикали на пустой участок до тех пор, пока полученная конфигурация не будет соответствовать целевой конфигурации (рис. 4.5). Рис. 4.5. Типичный экземпляр головоломки "игра в восемь". Решение имеет длину 26 этапов Средняя стоимость решения для сформированного случайным образом экземпляра головоломки "игра в восемь" составляет около 22 этапов. Коэффициент ветвления примерно равен 3. (Если пустой квадрат находится в середине коробки, то количество возможных ходов равно четырем, если находится в углу— двум, а если в середине одной из сторон — трем.) Это означает, что при исчерпывающем поиске на глубину 22 приходится рассматривать примерно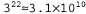 состояний. Отслеживая повторяющиеся состояния, это количество состояний можно сократить приблизительно в 170 000 раз, поскольку существует только 9 ! /2 = 181 440 различимых состояний, которые являются достижимыми (см. упр. 3.4.) Это количество состояний уже лучше поддается контролю, но соответствующее количество для игры в пятнадцать примерно равно состояний. Отслеживая повторяющиеся состояния, это количество состояний можно сократить приблизительно в 170 000 раз, поскольку существует только 9 ! /2 = 181 440 различимых состояний, которые являются достижимыми (см. упр. 3.4.) Это количество состояний уже лучше поддается контролю, но соответствующее количество для игры в пятнадцать примерно равно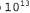 , поэтому для такой головоломки с более высокой сложностью требуется найти хорошую эвристическую функцию. Если нужно находить кратчайшие решения с использованием поиска А*, то требуется эвристическая функция, которая никогда не переоценивает количество этапов достижения цели. История исследований в области поиска таких эвристических функций для игры в пятнадцать является довольно долгой, а в данном разделе рассматриваются два широко используемых кандидата на эту роль, которые описаны ниже. , поэтому для такой головоломки с более высокой сложностью требуется найти хорошую эвристическую функцию. Если нужно находить кратчайшие решения с использованием поиска А*, то требуется эвристическая функция, которая никогда не переоценивает количество этапов достижения цели. История исследований в области поиска таких эвристических функций для игры в пятнадцать является довольно долгой, а в данном разделе рассматриваются два широко используемых кандидата на эту роль, которые описаны ниже. •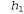 = количество фишек, стоящих не на своем месте. На рис. 4.5 все восемь фишек стоят не на своем месте, поэтому показанное слева начальное состояние имеет эвристическую оценку = количество фишек, стоящих не на своем месте. На рис. 4.5 все восемь фишек стоят не на своем месте, поэтому показанное слева начальное состояние имеет эвристическую оценку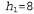 . Эвристическая функция . Эвристическая функция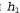 является допустимой, поскольку очевидно, что каждую фишку, находящуюся не на своем месте, необходимо переместить по меньшей мере один раз. является допустимой, поскольку очевидно, что каждую фишку, находящуюся не на своем месте, необходимо переместить по меньшей мере один раз. •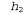 = сумма расстояний всех фишек от их целевых позиций. Поскольку фишки не могут передвигаться по диагонали, рассчитываемое расстояние представляет собой сумму горизонтальных и вертикальных расстояний. Такое расстояние иногда называют расстоянием, измеряемым в городских кварталах, или манхэттенским расстоянием. Эвристическая функция h2 также является допустимой, поскольку все, что может быть сделано в одном ходе, состоит лишь в перемещении одной фишки на один этап ближе к цели. Фишки от 1 до 8 в рассматриваемом начальном состоянии соответствуют такому значению манхэттенского расстояния: = сумма расстояний всех фишек от их целевых позиций. Поскольку фишки не могут передвигаться по диагонали, рассчитываемое расстояние представляет собой сумму горизонтальных и вертикальных расстояний. Такое расстояние иногда называют расстоянием, измеряемым в городских кварталах, или манхэттенским расстоянием. Эвристическая функция h2 также является допустимой, поскольку все, что может быть сделано в одном ходе, состоит лишь в перемещении одной фишки на один этап ближе к цели. Фишки от 1 до 8 в рассматриваемом начальном состоянии соответствуют такому значению манхэттенского расстояния: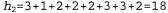 Как и можно было предположить, ни одна из этих функций не переоценивает истинную стоимость решения, которая равна 26.
|