Теперь мы можем применить многие идеи, изложенные в этой главе, для решения задач в мире вампуса, требующих использования вероятностных рассуждений (полное описание мира вампуса приведено в главе 7). Неопределенность в мире вампуса возникает из-за того, что датчики агента сообщают только частичную, локальную информацию об этом мире. Например, на рис. 13.2 показана ситуация, в которой каждый из трех достижимых квадратов ([1,3], [2,2] и [3,1]) может содержать яму. Чисто логический вывод не позволяет прийти к каким-либо заключениям о том, какой квадрат с наибольшей вероятностью окажется безопасным, поэтому логический агент может быть вынужден выбирать среди них случайным образом. В этом разделе будет показано, что вероятностный агент может действовать гораздо успешнее, чем логический агент.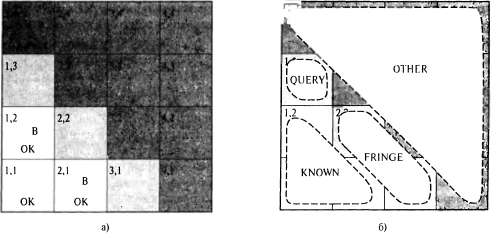

Рис. 13.2. Пример из мира вампуса: после обнаружения ветерка и в квадрате [1,2], и в квадрате [2,1] агент заходит в тупик — больше нет такого квадрата, который он мог бы обследовать без опасений (а); разделение квадратов на категории Known (Известные), Fringe (Периферийные) и Other (Другие) для формирования запроса (Query), касающегося квадрата [1,3] (б).

Наша цель будет состоять в том, чтобы вычислить вероятность наличия ямы в каждом из этих трех квадратов. (В данном конкретном примере игнорируется наличие вампуса и золота.) Относящиеся к этой задаче свойства мира вампуса состоят в том, что, во-первых, яма становится причиной возникновения ветерка во всех соседних квадратах, и, во-вторых, каждый квадрат, отличный от [1,3], содержит яму с вероятностью 0,2. Первый этап состоит в определении множества необходимых случайных переменных, как показано ниже.

•    Как и в случае пропозициональной логики, требуется по одной булевой переменнойдля каждого квадрата, которая принимает истинное значение тогда и только тогда, когда квадрат [ i, j ] действительно содержит яму.

•    Требуются также булевы переменные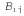, принимающие истинное значение тогда и только тогда, когда в квадрате [ i, j ] чувствуется ветерок; мы предусматриваем эти переменные только для наблюдаемых квадратов, в данном случае [1,1], [1,2] и [2,1].