Но интуиция подсказывает, что здесь есть какое-то упущение. Безусловно, напрашивается вопрос, не являются ли другие квадраты не относящимися к делу? Ведь содержимое квадрата [4,4] не влияет на то, имеется ли яма в квадрате [1,3]! И действительно, эта догадка является правильной. Пользуясь ею, предположим, что Fringe— переменные (отличные от переменной запроса), которые описывают свойства квадратов, соседних по отношению к посещенным квадратам; в данном случае таковыми являются только [2,2] и [3,1]. Кроме того, допустим, что Other— это переменные, которые относятся к другим неизвестным квадратам; в данном случае количество других квадратов равно 10, как показано на рис. 13.2, б. Ключевая идея состоит в том, что данные о наблюдаемом ветерке являются условно независимыми от других переменных, если даны условные переменные, переменные периферии и переменная запроса. После этой догадки остается лишь, так сказать, дело техники — выполнить несколько алгебраических операций.

Чтобы воспользоваться этой идеей, необходимо преобразовать формулу запроса в такую форму, в которой данные о наличии ветерка становятся условно зависимыми от всех других переменных, а затем упростить полученное выражение с использованием утверждения об условной независимости, как показано ниже.

В этом преобразовании на конечном этапе используется утверждение об условной независимости. Теперь первый терм в выражении не зависит от других переменных, поэтому можно переместить операцию суммирования внутрь выражения, следующим образом: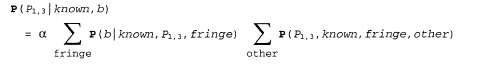

Согласно утверждению о независимости, соответствующему приведенному в уравнении 13.15, терм априорной вероятности может быть факторизован, после чего все эти термы могут быть переупорядочены следующим образом: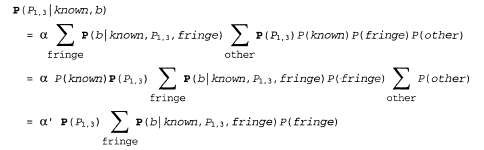