Следующий этап состоит в определении полного совместного распределения

. Применяя правило произведения, получаем следующее:

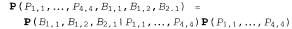
Эта декомпозиция позволяет очень легко определить, какими должны быть значения совместной вероятности. Первый терм представляет собой условную вероятность некоторой конфигурации данных о наличии ветерка, если дана конфигурация расположения ям; он принимает значение 1, если в квадратах, соседних с ямами, чувствуется ветерок, в противном случае принимает значение 0. Вторым термом является априорная вероятность конфигурации расположения ям. Каждый квадрат может содержать яму с вероятностью 0,2, независимо от других квадратов, поэтому имеет место следующее:

(13.15)

Для конфигурации с η ямами это значение равно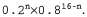

В ситуации, показанной на рис. 13.2, а, свидетельство состоит из наблюдаемого ветерка (или его отсутствия) в каждом посещенном квадрате, в сочетании с тем фактом, что каждый такой квадрат не содержит ямы. Эти факты можно сокращенно представить как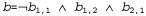иМы заинтересованы в получении ответов на такие запросы, какнасколько велика вероятность того, что квадрат [1,3] содержит яму, если даны результаты всех наблюдений, сделанных до сих пор?

Для получения ответа на этот запрос можно воспользоваться стандартным подходом, основанном на уравнении 13.6 и реализованном в алгоритме Enumerate-Joint-Ask, а именно просуммировать элементы из таблицы полного совместного распределения. Допустим, что Unknown (Неизвестное) — составная переменная, которая состоит из переменных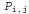для квадратов, отличных от квадратов Known и квадрата запроса [1,3]. В таком случае с помощью уравнения 13.6 получаем следующее:

Полное совместное распределение вероятностей уже было задано, поэтому задача решена, точнее, осталось только выполнить вычисления. Количество неизвестных квадратов равно 12, поэтому требуемая сумма состоит из=409 6 термов. Вообще говоря, количество термов в этой сумме растет экспоненциально в зависимости от количества квадратов.