|
Страница 1 из 2 В основе двунаправленного поиска лежит такая идея, что можно одновременно проводить два поиска (в прямом направлении, от начального состояния, и в обратном направлении, от цели), останавливаясь после того, как два процесса поиска встретятся на середине (рис. 3.10). Дело в том, что значение 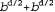 гораздо меньше, чем гораздо меньше, чем  , или, как показано на этом рисунке, площадь двух небольших кругов меньше площади одного большого круга с центром в начале поиска, который охватывает цель поиска. , или, как показано на этом рисунке, площадь двух небольших кругов меньше площади одного большого круга с центром в начале поиска, который охватывает цель поиска. Рис. 3.10. Схематическое представление двунаправленного поиска в том состоянии, когда он должен вскоре завершиться успешно после того, когда одна из ветвей, исходящих из начального узла, встретится с ветвью из целевого узла Двунаправленный поиск реализуется с помощью метода, в котором предусматривается проверка в одном или в обоих процессах поиска каждого узла перед его развертыванием для определения того, не находится ли он на периферии другого дерева поиска; в случае положительного результата проверки решение найдено. Например, если задача имеет решение на глубине d=6 и в каждом направлении осуществляется поиск в ширину с последовательным развертыванием по одному узлу, то в самом худшем случае эти два процесса поиска встретятся, если в каждом из них будут развернуты все узлы на глубине 3, кроме одного. Это означает, что при b=10 будет сформировано общее количество узлов, равное 22 200, а не 11 111 100, как при стандартном поиске в ширину. Проверка принадлежности узла к другому дереву поиска может быть выполнена за постоянное время с помощью хэш-таблицы, поэтому временная сложность двунаправленного поиска определяется как 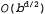 . В памяти необходимо хранить по крайней мере одно из деревьев поиска, для того, чтобы можно было выполнить проверку принадлежности к другому дереву, поэтому пространственная сложность также определяется как . В памяти необходимо хранить по крайней мере одно из деревьев поиска, для того, чтобы можно было выполнить проверку принадлежности к другому дереву, поэтому пространственная сложность также определяется как 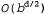 . Такие требования к пространству являются одним из наиболее существенных недостатков двунаправленного поиска. Этот алгоритм является полным и оптимальным (при единообразных стоимостях этапов), если оба процесса поиска осуществляются в ширину; другие сочетания методов могут характеризоваться отсутствием полноты, оптимальности или того и другого. . Такие требования к пространству являются одним из наиболее существенных недостатков двунаправленного поиска. Этот алгоритм является полным и оптимальным (при единообразных стоимостях этапов), если оба процесса поиска осуществляются в ширину; другие сочетания методов могут характеризоваться отсутствием полноты, оптимальности или того и другого.
<< В начало < Предыдущая 1 2 Следующая > В конец >>
|