К счастью, возможно более полезное обобщение, называемое стохастическим доминированием, которое встречается очень часто в реальных задачах. Принцип стохастического доминирования проще понять в контексте задачи с одним атрибутом. Допустим, исследования показали, что стоимость строительства аэропорта на площадке S1 равномерно распределена в пределах от 2,8 миллиарда долларов до 4,8 миллиарда долларов, а стоимость строительства на площадке S2 равномерно распределена в пределах от 3 миллиардов долларов до 5,2 миллиарда долларов. На рис. 16.4, а показаны эти распределения в виде графиков, на которых указанные значения отображены в виде отрицательных значений. В таком случае при наличии лишь той информации, что полезность уменьшается с увеличением стоимости, можно прийти к заключению, что вариант S1 стохастически доминирует над вариантом S2 (и поэтому вариант S2 может быть отброшен). Важно отметить, что такой вывод не следует из сравнения ожидаемых затрат. Например, если бы было известно, что стоимость варианта S1 точно равна 3,8 миллиарда долларов, то мы не смогли бы принять решение без дополнительной информации о полезности денег.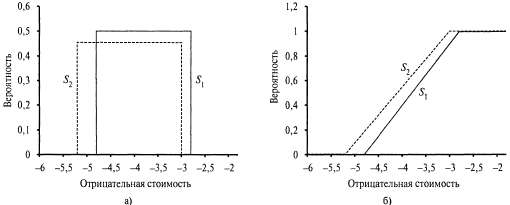

Рис. 16.4. Стохастическое доминирование: вариант S1 стохастически доминирует над вариантом S2 no стоимости (а); кумулятивные распределения для отрицательной стоимости вариантов S1 и S2 (б)