В разделе 25.2 введено понятие динамического состояния, которое расширяет представление о кинематическом состоянии робота, позволяя моделировать скорости робота. Например, в описании динамического состояния, кроме данных об угле поворота шарнира робота, отражена скорость изменения этого угла. В модели перехода для любого представления динамического состояния учитываются влияния усилий на эту скорость изменения. Подобные модели обычно выражаются с помощью дифференциальных уравнений, которые связывают количество (например, кинематическое состояние) с изменением этого количества во времени (например, скоростью). В принципе, можно было бы выбрать способ планирования движений робота с использованием динамических моделей вместо кинематических моделей, которые рассматривались в предыдущих разделах. Такая методология приводит к достижению превосходных показателей производительности робота, если удается составить нужные планы. Однако динамическое состояние намного сложнее по сравнению с кинематическим пространством, а из-за большого количества измерений задачи планирования движений становятся неразрешимыми для любых роботов, кроме самых простых. По этой причине применяемые на практике робототехнические системы часто основаны на использовании более простых кинематических планировщиков пути.

Общепринятым методом компенсации ограничений кинематических планов является использование для слежения за роботом отдельного механизма, контроллера. Контроллерами называются устройства, вырабатывающие команды управления роботом в реальном времени с использованием обратной связи от среды для достижения цели управления. Если цель состоит в удержании робота на заранее запланированном пути, то такие контроллеры часто называют опорными контроллерами, а путь называют опорным путем. Контроллеры, оптимизирующие глобальную функцию затрат, называют оптимальными контроллерами. По существу, оптимальная политика для задачи MDP является определением оптимального контроллера.

На первый взгляд задача управления, позволяющая удерживать робот на заранее заданном пути, кажется относительно простой. Но на практике даже в ходе решения этой внешне простой задачи могут встретиться некоторые ловушки. На рис. 25.19, а показано, какие нарушения могут при этом возникать. На данном рисунке демонстрируется путь робота, предпринимающего попытку следовать по кинематическому пути. После возникновения любого отклонения (обусловленного либо шумом, либо ограничениями на те усилия, которые может применять робот) робот прикладывает противодействующее усилие, величина которого пропорциональна этому отклонению. Интуитивные представления говорят о том, что такой подход якобы вполне оправдан, поскольку отклонения должны компенсироваться противодействующим усилием, чтобы робот не отклонялся от своей траектории. Однако, как показано на рис. 25.19, a, действия такого контроллера вызывают довольно интенсивную вибрацию робота. Эта вибрация является результатом естественной инерции манипулятора робота — робот, резко направленный в стороны опорной позиции, проскакивает эту позицию, что приводит к возникновению симметричной погрешности с противоположным знаком. Согласно кривой, приведенной на рис. 25.19, а, такое перерегулирование может продолжаться вдоль всей траектории, поэтому результирующее движение робота далеко от идеального. Очевидно, что нужно предусмотреть лучший способ управления.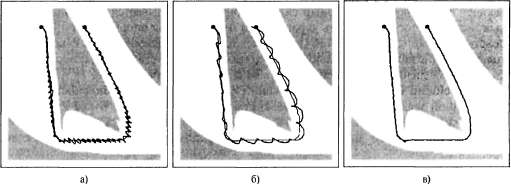

Рис. 25.19. Управление манипулятором робота с использованием различных методов: пропорциональное управление с коэффициентом усиления 1.0 (а); пропорциональное управление с коэффициентом усиления О,1 (б); пропорционально-дифференциальное управление с коэффициентами усиления 0,3 для пропорционального и 0,8 для дифференциального компонента (в). Во всех случаях предпринимается попытка провести манипулятор робота по пути, обозначенному серым цветом