Динамической байесовской сетью, или сокращенно DBN (Dynamic Bayesian Network), называется байесовская сеть, которая представляет временную вероятностную модель такого типа, как описано в разделе 15.1. В данной главе уже рассматривались примеры сетей DBN: сеть для задачи с зонтиком (см. рис. 15.2) и сеть фильтра Калмана (см. рис. 15.5). Вообще говоря, каждый временной срез сети DBN может иметь любое количество переменных состояния xt и переменных свидетельства Et. Для упрощения мы будем предполагать, что переменные и связи между ними точно тиражируются от среза к срезу и что сеть DBN представляет марковский процесс первого порядка, так что каждая переменная может иметь родительские переменные только в своем собственном временном срезе или в непосредственно предшествующем временном срезе.

Должно быть очевидно, что любая скрытая марковская модель может быть представлена в виде сети DBN с единственной переменной состояния и с единственной переменной свидетельства. Справедливо также утверждение, что каждая сеть DBN с дискретными переменными может быть представлена в виде модели НММ; как было описано в разделе 15.3, можно скомбинировать все переменные состояния в сети DBN в одну переменную состояния, значениями которой являются все возможные кортежи значений отдельных переменных состояния. Итак, если каждая модель НММ представляет собой сеть DBN, а каждая сеть DBN может быть преобразована в модель НММ, то в чем состоит различие между ними? Это различие заключается в том, что благодаря декомпозиции состояния сложной системы на со-ставляющие его переменные сеть DBN позволяет воспользоваться преимуществами разреженности временной вероятностной модели. Предположим, например, что в сети DBN имеется 20 булевых переменных состояния, каждая из которых имеет три родительских переменных в предшествующем срезе. 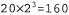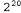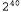В таком случае модель перехода DBN включаетвероятностей, а соответствующая модель НММ имеет состояний и поэтому(или примерно триллион) вероятностей в матрице перехода. Такая ситуация неприемлема по меньшей мере по трем причинам: во-первых, требуется гораздо больше пространства для самой модели НММ; во-вторых, из-за огромной матрицы перехода вероятностный вывод с помощью модели НММ становится гораздо более дорогостоящим; и, в-третьих, из-за проблем, связанных с изучением такого огромного количества параметров, чистая модель НММ становится непригодной для решения крупных задач. Связь между сетями DBN и моделями НММ примерно аналогична связи между обычными байесовскими сетями и полностью табулированными совместными распределениями.