2.    Пустое множество не имеет присоединенных к нему элементов, иными словами, не существует способа разложения множества Empty Set на меньшее множество и еще один элемент: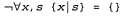

3.    Присоединение к множеству элемента, уже имеющегося в этом множестве, не оказывает никакого эффекта: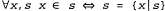

4.    Единственными элементами множества являются элементы, которые были к нему присоединены. Мы выразим эту мысль рекурсивно, утверждая, что х — элемент множества s тогда и только тогда, когда s эквивалентно некоторому множеству s2, к которому присоединен некоторый элемент у, где либо у совпадает с х, либо χ является элементом s2:

5.    Множество является подмножеством другого множества тогда и только тогда, когда все элементы первого множества являются элементами второго множества: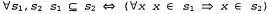

6.   Два множества равны тогда и только тогда, когда каждое из них является подмножеством другого: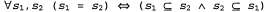

7.    Некоторый объект принадлежит к пересечению двух множеств тогда и только тогда, когда он является элементом обоих этих множеств:

8.    Некоторый объект принадлежит к объединению двух множеств тогда и только тогда, когда он является элементом того или другого множества: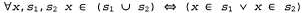

Списки подобны множествам. Различия между ними состоят в том, что списки упорядочены, а один и тот же элемент может появляться в списке несколько раз. Для списков может использоваться словарь ключевых слов Lisp: Nil — это список-константа без элементов; Cons, Append, First и Rest — функции; Find— предикат, который выполняет для списков такие же функции, какие Member выполняет для множеств. List? — предикат, принимающий истинное значение только при получении параметра, представляющего собой список. Как и в случае множеств, обычно принято использовать синтаксические упрощения в логических высказываниях, в которых применяются списки. Пустой список обозначается как [ ]. Терм Cons (χ, у), где у— непустой список, записывается как [х|у]. Терм Cons(x,Nil) (т.е. список, содержащий только элемент х) записывается как [х]. Список из нескольких элементов, такой как [А, в, С], соответствует вложенному терму Cons (A, Cons (B, Cons (С, Nil))).