Проблемы представления времени, изменений, действий и событий широко исследовались не только в искусственном интеллекте, но и в философии и теоретических компьютерных науках. К числу наиболее развитых направлений относится временная логика, представляющая собой специализированную логику, в которой каждая модель описывает полную траекторию развития процесса во времени (обычно либо линейную, либо ветвящуюся), а не просто статическую реляционную структуру. 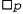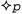Эта логика включает модальные операторы, применяемые к формулам; означает "р будет истинным во все времена в будущем", аозначает "р станет истинным в некоторый момент в будущем". Исследования в области временной логики были впервые начаты Аристотелем, а также представителями мегарской и стоической школ в древней Греции. В современной истории развития науки применение формального исчисления для проведения рассуждений о времени было впервые предложено Финдлеем [468], но считается, что наибольшее влияние оказала работа Артура Прайора [1239]. К учебникам по временной логике относятся [1283] и [1529].

Специалисты в области теоретических компьютерных наук уже давно стремились формально описать свойства программ, рассматриваемых как последовательности вычислительных действий. Бурстолл [210] выдвинул идею использования модальных операторов для формирования рассуждений о компьютерных программах. Вскоре после этого Воган Пратт [1233] разработал динамическую логику, в которой модальные операторы обозначают результаты выполнения программ или другие действия (см. также [620]). Например, в динамической логике, если а— имя программы, то " [а]р" означает "р должно быть истинным во всех состояниях мира, ставших результатом выполнения программы α в текущем состоянии мира", а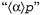означает "р должно быть истинным по меньшей мере в одном из состоянии мира, ставшим результатом выполнения программы α в текущем состоянии мира". Динамическая логика была применена для фактического анализа программ Фишером и Ладнером [472]. В [1218] предложена идея использования классической временной логики для формирования рассуждений о программах.