Развитие алгоритмов Монте-Карло на основе цепи Маркова (Markov chain Monte Carlo — MCMC) началось с создания алгоритма Метрополиса, впервые опубликованного в статье [1036], которая стала также первой публикацией сведений об алгоритме эмуляции отжига (см. главу 4). Формирователь выборок Гиббса был предложен в [535] для вероятностного вывода в неориентированных сетях Маркова. Применение алгоритма МСМС к байесовским сетям было предложено Перлом [1190]. Статьи, собранные в [554], охватывают широкий диапазон направлений использования алгоритма МСМС, многие из которых были разработаны при создании широко известного пакета Bugs [555].

В этой главе не рассматривались два очень важных семейства методов аппроксимации. Первым из них является семейство методов вариационной аппроксимации, которые могут использоваться для упрощения сложных вычислений любых типов. Основная идея состоит в том, что должна быть предложена сокращенная версия первоначальной задачи, с которой легче работать, но которая напоминает первоначальную задачу настолько близко, насколько это возможно. Сокращенная задача описывается с помощью некоторых вариационных параметров λ, которые корректируются с целью минимизации функции расстояния D между оригинальной и сокращенной задачами, часто путем решения системы уравнений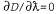. Во многих случаях могут быть получены строгие верхние и нижние границы. Вариационные методы уже давно использовались в статистике [1333]. В статистической физике метод поля осредненных величин (mean field) представляет собой особую вариационную аппроксимацию, в которой предполагается, что отдельные переменные, входящие в состав модели, являются полностью независимыми. Эта идея была применена для поиска решений в крупных неориентированных сетях Маркова [1174], [1209]. В [1353] представлены результаты разработки математических основ применения вариационных методов к байесовским сетям и получения точных аппроксимаций нижней границы для сигмоидальных сетей с использованием методов поля осредненных величин. Эта методология была дополнена в [720] для получения нижней и верхней границ. Обзор вариационных подходов приведен в [748].