|
Страница 2 из 2 Вторая проблема состоит в том, что алгоритмы обычно не поддаются точному анализу. В этом случае приходится прибегать к аппроксимации и использовать, например, такую формулировку, что быстродействие алгоритма Summation характеризуется величиной О(п). Это означает, что быстродействие алгоритма измеряется величиной, пропорциональной п, возможно, за исключением нескольких небольших значений п. Более формально это определение можно представить с помощью следующей формулы: 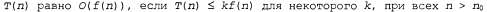
Перейдя к использованию системы обозначений 0(), мы получаем возможность воспользоваться так называемым асимптотическим анализом. А в рамках этого подхода можно, например, безоговорочно утверждать, что если η асимптотически приближается к бесконечности, то алгоритм, характеризующийся показателем О(п), проявляет себя лучше по сравнению с алгоритмом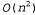 , тогда как единственное число, полученное с помощью эталонного тестирования, не может служить обоснованием подобного утверждения. , тогда как единственное число, полученное с помощью эталонного тестирования, не может служить обоснованием подобного утверждения. Система обозначений О () позволяет создать абстрактное представление, в котором не учитываются постоянные коэффициенты, благодаря чему она становится более простой в использовании, но менее точной, чем система обозначений т[). Например, в конечном итоге алгоритм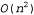 всегда будет считаться худшим по сравнению с алгоритмом О(п), но если бы эти два алгоритма характеризовались значениями всегда будет считаться худшим по сравнению с алгоритмом О(п), но если бы эти два алгоритма характеризовались значениями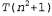 и Т(100л+1000), то фактически алгоритм и Т(100л+1000), то фактически алгоритм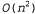 был бы лучше при был бы лучше при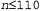 Несмотря на этот недостаток, асимптотический анализ представляет собой инструментальное средство, наиболее широко используемое для анализа алгоритмов. Этот метод можно считать достаточно точным, поскольку в процессе анализа создается абстрактное представление и для точного количества операций (поскольку игнорируется постоянный коэффициент k), и для точного содержимого входных данных (поскольку рассматривается исключительно их объем л); благодаря этому анализ становится осуществимым с помощью математических методов. Система обозначений О () представляет собой хороший компромисс между точностью и простотой анализа.
<< В начало < Предыдущая 1 2 Следующая > В конец >>
|