Описанный выше алгоритм устранения переменной является простым и эффективным средством получения ответов на отдельные запросы. Если же возникает необходимость вычислить апостериорные вероятности для всех переменных в сети, то этот алгоритм может оказаться менее эффективным. Например, в сети с полидревовидной структурой для этого потребуется выдать О(n) запросов со стоимостью О(n) каждый, что в сумме составляет затраты времен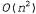и. Использование алгоритмов кластеризации (известных также под названием алгоритмов дерева соединения-join tree), позволяет сократить это время до 0(п). По указанной причине данные алгоритмы широко используются в коммерческих инструментальных средствах на основе байесовских сетей.

Основная идея кластеризации состоит в том, что отдельные узлы в дереве должны быть соединены для формирования кластерных вершин таким образом, чтобы результирующая сеть стала полидеревом. Например, многосвязная сеть, показанная на рис. 14.9, а, может быть преобразована в полидерево путем объединения вершин Sprinkler (Опрыскиватель) и Rain (Дождь) в кластерную вершину, называемую Sprinklers Rain (см. рис. 14.9, б). Эти две булевы вершины заменяются мегавер-шиной, которая принимает четыре возможных значения: тт, TF, FT и FF. Данная мегавершина имеет только одну родительскую вершину— булеву переменную Cloudy, поэтому для нее количество обусловливающих случаев равно двум.

Рис. 14.9. Пример применения кластеризации: многосвязная сеть с таблицами условных вероятностей (а); кластеризованный эквивалент многосвязной сети (б)

После преобразования сети в форму полидерева применяется алгоритм вероятностного вывода специального назначения. По сути этот алгоритм представляет собой одну из форм алгоритма распространения ограничений (см. главу 5), где ограничения обеспечивают согласование соседних кластеров по апостериорной вероятности любых переменных, которые являются в них общими. При наличии тщательно продуманных средств учета этот алгоритм позволяет вычислять апостериорные вероятности для всех вершин в сети, отличных от вершин свидетельства, за время О(n), где n теперь обозначает размер модифицированной сети. Тем не менее NP-трудность решаемой задачи не исчезает: если сеть требует экспоненциальных затрат времени и пространства при устранении переменной, то экспоненциальные затраты времени и пространства требуются и для построения таблиц СРТ в кластеризованной сети.