Описанный выше алгоритм перебора можно существенно улучшить, исключив повторные вычисления такого типа, как показано на рис. 14.8. Его идея проста: выполнить вычисление один раз и сохранить результаты для дальнейшего использования. В этом выражается одна из форм динамического программирования. Существует несколько версий такого подхода; в данной главе будет представлен алгоритм устранения переменной (variable elimination), который является наиболее простым. Устранение переменной осуществляется путем вычисления выражений, подобных представленному в уравнении 14.3, в порядке справа налево (т.е. на рис. 14.8 — сверху вниз). Промежуточные результаты сохраняются, а операции суммирования по каждой переменной выполняются только для тех частей выражения, которые зависят от этой переменной.

Проиллюстрируем этот процесс на примере сети с описанием взлома. Нам необходимо вычислить следующее выражение: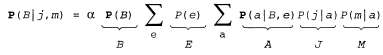

Обратите внимание на то, что каждая часть этого выражения аннотирована именем связанной с ней переменной; эти части называются факторами. Этапы работы алгоритма устранения переменной описаны ниже.

•    Фактор для, не требует суммирования по Μ (поскольку значение Μ уже фиксировано). Мы сохраним эту вероятность при условии, что задано каждое значение а в виде следующего двухэлементного вектора: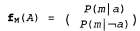

(Обозначение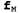показывает, что для получения f используется м.)

•    Аналогичным образом сохраняется фактор для J в виде двухэлементного вектора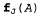

•    Фактор для А выражается распределением, которое представляет собой матрицу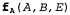с размерами 2x2x2.

•    Теперь необходимо устранить путем суммирования из произведения этих трех факторов переменную А, что позволит получить матрицу 2x2, индексы которой пробегают только по в и Е. Поместим штрих над А в имени этой матрицы для указания на то, что А устранена путем суммирования: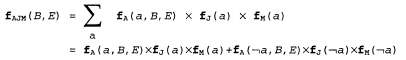

Применяемый в этом выражении процесс умножения называется процессом получения точечного произведения (pointwise product) и будет вскоре описан.

•    Обработаем таким же образом переменную E: исключим Ε путем суммирования из произведения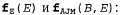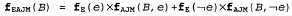

•    Теперь мы можем вычислить ответ, умножив фактор для на накопленную матрицу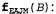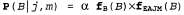

В упр. 14.7, α предлагается проверить, действительно ли данный процесс приводит к получению правильного ответа.