|
Страница 2 из 2 Исследуя приведенную выше последовательность этапов, можно убедиться в том, что требуются две основные вычислительные операции: получение точечного произведения пары факторов и исключение некоторой переменной путем суммирования из произведения факторов. Точечное произведение — это не результат умножения матриц и не результат поэлементного умножения. Точечное произведение двух факторов,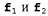 , представляет собой новый фактор f, переменные которого являются объединением переменных из , представляет собой новый фактор f, переменные которого являются объединением переменных из . Предположим, что два фактора имеют общие переменные . Предположим, что два фактора имеют общие переменные  . В таком случае получим следующее: . В таком случае получим следующее: 
Если все переменные являются бинарными, то факторы f 1 и f 2 имеют элементов соответственно, а точечное произведение включает элементов соответственно, а точечное произведение включает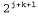 элементов. Например, если даны два фактора, элементов. Например, если даны два фактора,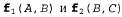 , с распределениями вероятностей, показанными ниже, то точечное произведение , с распределениями вероятностей, показанными ниже, то точечное произведение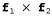 задается в табл. 14.2 как задается в табл. 14.2 как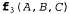 Таблица 14.2. Пример произведения факторов  Операция исключения некоторой переменной путем суммирования из произведения факторов также является несложной. Единственное затруднение заключается в следующем: в этой операции необходимо учитывать, что любой фактор, который не зависит от переменной, подлежащей исключению путем суммирования, может быть вынесен за пределы выражения суммирования, например, как показано ниже.  Теперь вычисляется точечное произведение в выражении суммирования и переменная исключается путем суммирования из результирующей матрицы следующим образом: 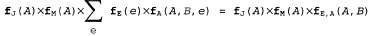
Обратите внимание на то, что матрицы не умножаются до тех пор, пока не потребуется исключить некоторую переменную путем суммирования из накопленного произведения. В данный момент умножаются только те матрицы, которые включают переменную, подлежащую исключению путем суммирования. Если даны процедуры получения точечного произведения и исключения путем суммирования, то сам алгоритм устранения переменной может быть записан весьма просто, как показано в листинге 14.2. Листинг 14.2. Алгоритм устранения переменной, предназначенный для получения ответов на запросы в байесовских сетях 
Рассмотрим еще один запрос: P{JohnCalls| Burglary = true). Как обычно, на первом этапе необходимо записать вложенное выражение суммирования: 
Если бы мы вычисляли это выражение справа налево, то заметили бы нечто интересное: терм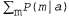 равен 1 по определению! Поэтому сразу отпадает необходимость учитывать это выражение; переменная Мне имеет отношения к данному запросу. Эту мысль можно выразить иным образом: результат запроса P{JohnCalls| Burglary- true) не изменится, если из сети вообще будет исключена переменная MaryCalls. Вообще говоря, из сети может быть удалена любая листовая вершина, если она не относится к переменной запроса или к переменной свидетельства. После ее удаления могут еще оставаться некоторые листовые вершины, которые также могут не относится к данному запросу. Продолжая указанный процесс, мы в конечном итоге обнаружим, что к запросу не относится любая переменная, которая не является потомком переменной запроса или переменной свидетельства. Поэтому алгоритм устранения переменной позволяет удалять все эти переменные, прежде чем приступать к вычислению ответа на запрос. равен 1 по определению! Поэтому сразу отпадает необходимость учитывать это выражение; переменная Мне имеет отношения к данному запросу. Эту мысль можно выразить иным образом: результат запроса P{JohnCalls| Burglary- true) не изменится, если из сети вообще будет исключена переменная MaryCalls. Вообще говоря, из сети может быть удалена любая листовая вершина, если она не относится к переменной запроса или к переменной свидетельства. После ее удаления могут еще оставаться некоторые листовые вершины, которые также могут не относится к данному запросу. Продолжая указанный процесс, мы в конечном итоге обнаружим, что к запросу не относится любая переменная, которая не является потомком переменной запроса или переменной свидетельства. Поэтому алгоритм устранения переменной позволяет удалять все эти переменные, прежде чем приступать к вычислению ответа на запрос.
<< В начало < Предыдущая 1 2 Следующая > В конец >>
|