|
Страница 1 из 2 Уравнение Беллмана является основой алгоритма итерации по значениям, применяемого для решения задач MDP. Если существует n возможных состояний, то количество уравнений Беллмана также равно п, по одному для каждого состояния. Эти η уравнений содержат η неизвестных — полезностей состояний. Поэтому можно было бы заняться поиском решений системы этих уравнений, чтобы определить полезности. Тем не менее возникает одна проблема, связанная с тем, что эти уравнения являются нелинейными, поскольку оператор "max" — это нелинейный оператор. Системы линейных уравнений могут быть решены очень быстро с использованием методов линейной алгебры, а для решения систем нелинейных уравнений необходимо преодолеть некоторые проблемы. Один из возможных подходов состоит в использовании итерационных методов. Для этого нужно начать с произвольных исходных значений полезностей, вычислить правую часть уравнения и подставить ее в левую, тем самым обновляя значение полезности каждого состояния с учетом полезностей его соседних состояний. Такая операция повторяется до тех пор, пока не достигается равновесие. Допустим, что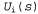 — это значение полезности для состояния s в i-й итерации. Шаг итерации, называемый обновлением Беллмана, выглядит следующим образом: — это значение полезности для состояния s в i-й итерации. Шаг итерации, называемый обновлением Беллмана, выглядит следующим образом: 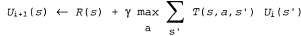 (17.6) (17.6)
Если обновление Беллмана используется неопределенно большое количество раз, то гарантируется достижение равновесия (см. следующий подраздел), и в этом случае конечные значения полезности должны представлять собой решения уравнений Беллмана. В действительности они также представляют собой уникальные решения, и соответствующая стратегия (полученная с помощью уравнения 17.4) является оптимальной. Применяемый при этом алгоритм, называемый Value-Iteration, показан в листинге 17.1. Листинг 17.1. Алгоритм итерации по значениям для вычисления полезностей состояний. Условие завершения работы взято из уравнения 17.8 
<< В начало < Предыдущая 1 2 Следующая > В конец >>
|