До сих пор в этой главе был определен синтаксис для высказываний, а также для априорных и условных вероятностных утверждений об этих высказываниях. Теперь необходимо определить своего рода семантику для вероятностных утверждений. Начнем с базовых аксиом, которые служат для определения шкалы вероятностей и ее конечных точек, как описано ниже.

1.    Все вероятности находятся в пределах от 0 до 1; для любого высказывания а справедливо следующее: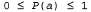

2.    Безусловно истинные (т.е. выполнимые) высказывания имеют вероятность 1, а безусловно ложные (т.е. невыполнимые) высказывания имеют вероятность 0:

Кроме того, требуется аксиома, которая соединяет вероятности логически взаимосвязанных высказываний. Такую аксиому можно проще всего составить, определив вероятность дизъюнкции, как показано ниже.

3.    Вероятность дизъюнкции задается следующей формулой:

Это правило можно легко запомнить, отметив, что те случаи, когда высказывание а является истинным, вместе с теми случаями, когда b является истинным, безусловно, охватывают все те случаи, когда истинно высказывание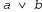; но в сумме двух множеств случаев их пересечение встречается дважды, поэтому необходимо вычесть

Эти три аксиомы часто называют аксиомами Колмогорова в честь советского математика Андрея Колмогорова, который показал, как построить остальную часть теории вероятностей на этом простом фундаменте. Обратите внимание на то, что в этих аксиомах речь идет только об априорных вероятностях, а не об условных; это связано с тем, что последние уже были определены в терминах первых в уравнении 13.1.