|
Страница 5 из 5 Осталась еще одна проблема, которую мы до сих пор тщательно обходили, — вопрос об ацикличности. Логическая схема является ацикличной, если каждый путь, соединяющий выход некоторого регистра в обратном направлении с его входом, содержит промежуточный элемент задержки. Мы требуем, чтобы все схемы были ацикличными, поскольку логические схемы, являющиеся цикличными, не работают как физические устройства! Они могут переходить в режим неустойчивых колебаний, что приводит к появлению неопределенных значений. В качестве примера цикличной схемы рассмотрим следующий дополненный вариант уравнения 7.6: 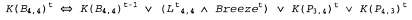 (7.9) (7.9)
Дополнительные дизъюнкты,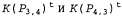 , позволяют агенту определить, чувствуется ли ветерок, на основании известных данных о наличии ям в соседних квадратах, и, на первый взгляд, в этом нет ничего предосудительного. Но, к сожалению, появление ветерка зависит от наличия ям в соседних квадратах, а наличие ям зависит от того, чувствуется ли ветерок в соседних квадратах, и такая связь устанавливается с помощью уравнений, подобных уравнению 7.8. Поэтому полная логическая схема будет содержать циклы. , позволяют агенту определить, чувствуется ли ветерок, на основании известных данных о наличии ям в соседних квадратах, и, на первый взгляд, в этом нет ничего предосудительного. Но, к сожалению, появление ветерка зависит от наличия ям в соседних квадратах, а наличие ям зависит от того, чувствуется ли ветерок в соседних квадратах, и такая связь устанавливается с помощью уравнений, подобных уравнению 7.8. Поэтому полная логическая схема будет содержать циклы. Сложность здесь заключается не в том, что дополненное уравнение 7.9 стало неправильным. Скорее всего, проблема состоит в том, что промежуточные зависимости, представленные подобными уравнениями, невозможно разрешить с помощью распространения истинностных значений по соответствующим логическим схемам. Ациклическая версия схемы, составленной с использованием уравнения 7.6, которая определяет наличие ветерка только с помощью прямого наблюдения, является неполной в том смысле, что могут возникать такие ситуации, когда агент на основе логической схемы окажется менее осведомленным, чем агент на основе логического вывода, использующий полную процедуру логического вывода. Например, если чувствуется ветерок в квадрате [1,1], то агент на основе логического вывода может прийти к заключению, что ветерок чувствуется также в квадрате [2,2], а агент на основе ациклической логической схемы, использующий уравнение 7.6, на это не способен. Задача создания полной логической схемы выполнима (в конце концов, логические схемы дают возможность эмулировать любой цифровой компьютер), но такая схема окажется значительно более сложной по сравнению с ациклической логической схемой.
<< В начало < Предыдущая 1 2 3 4 5 Следующая > В конец >>
|