|
Вероятность — это мера, заданная на множестве событий, которая удовлетворяет трем приведенным ниже аксиомам. 1. Мера каждого события находится в пределах от 0 до 1. Это утверждение записывается как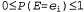 , где Е — случайная переменная, представляющая событие; , где Е — случайная переменная, представляющая событие;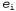 — возможные значения Е. Вообще говоря, случайные переменные обозначаются прописными буквами, а их значения — строчными. — возможные значения Е. Вообще говоря, случайные переменные обозначаются прописными буквами, а их значения — строчными. 2. Мера всего множества равна 1; это означает, что 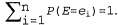
3. Вероятность объединения несовместимых событий равна сумме вероятностей отдельных событий; это означает, что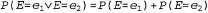 , где , где 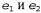 являются несовместимыми. являются несовместимыми.
Вероятностная модель состоит из пространства выборок взаимоисключающих возможных результатов, наряду с вероятностной мерой для каждого результата. Например, в модели погоды на завтра результатами могут быть sunny (солнце), cloudy (облачность), rainy (дождь) и snowy (снег). Подмножество этих результатов представляет собой событие. Например, событие выпадения осадков — это подмножество {rainy, snowy}. Для обозначения вектора значений используется терм Ρ (Ε). Кроме того, используется терм Ρ (Ε). Кроме того, применяется как сокращенное обозначение для применяется как сокращенное обозначение для , а служит для обозначения , а служит для обозначения 
Условная вероятность Р{В|А) определяется как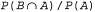 . Переменные А и в являются условно независимыми, если р(в|а)=р(В) (или, равным образом, если р[а|в) =Р{А)). Непрерывные переменные имеют бесконечное количество значений, и если распределение вероятностей этих значений не характеризуется наличием пиковых значений в отдельных точках, то вероятность любого отдельно взятого значения равна 0. Поэтому определим функцию плотности вероятностей, которая также обозначается как Ρ (X), но имеет немного иной смысл по сравнению с дискретной функцией вероятностей Р{А). Функция плотности вероятностей Ρ(Х=с) определяется как отношение вероятности того, что X попадает в интервал вокруг с, к ширине этого интервала, измеряемая в пределе приближения ширины интервала к нулю: . Переменные А и в являются условно независимыми, если р(в|а)=р(В) (или, равным образом, если р[а|в) =Р{А)). Непрерывные переменные имеют бесконечное количество значений, и если распределение вероятностей этих значений не характеризуется наличием пиковых значений в отдельных точках, то вероятность любого отдельно взятого значения равна 0. Поэтому определим функцию плотности вероятностей, которая также обозначается как Ρ (X), но имеет немного иной смысл по сравнению с дискретной функцией вероятностей Р{А). Функция плотности вероятностей Ρ(Х=с) определяется как отношение вероятности того, что X попадает в интервал вокруг с, к ширине этого интервала, измеряемая в пределе приближения ширины интервала к нулю: 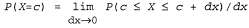
Функция плотности должна быть неотрицательной при всех χ и соответствовать следующему требованию: 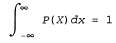
Может быть также определена ^ кумулятивная функция плотности вероятностей F (X), которая представляет собой вероятность того, что некоторая случайная переменная меньше х: 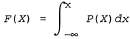
Следует отметить, что функция плотности вероятностей измеряется в определенных единицах, а дискретная функция вероятностей является безразмерной. Например, если переменная X измеряется в секундах, то плотность измеряется в Гц (т.е. 1/с). Если X— точка в трехмерном пространстве, измеряемом в метрах, то плотность измеряется в 1/м3. Одним из наиболее важных распределений вероятностей является гауссово распределение, известное также под названием нормального распределения. Гауссово распределение со средним μ и среднеквадратичным отклонением σ (и поэтому с дисперсией ) определяется следующей формулой: ) определяется следующей формулой: 
где х— непрерывная переменная, изменяющаяся в пределах от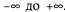 . Если среднее μ=0 и дисперсия . Если среднее μ=0 и дисперсия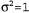 , то имеет место частный случай нормального распределения, называемый стандартным нормальным распределением. Если распределение задано на векторе x в пространстве с d измерениями, то оно представляет собой многомерное гауссово распределение: , то имеет место частный случай нормального распределения, называемый стандартным нормальным распределением. Если распределение задано на векторе x в пространстве с d измерениями, то оно представляет собой многомерное гауссово распределение: 
где μ — вектор средних; Σ — матрица ковариации этого распределения. При наличии одного измерения можно также определить функцию кумулятивного распределения F(x) как вероятность того, что случайная переменная будет меньше чем х. Для стандартного нормального распределения эта функция задается следующим образом: 
где erf(x) — так называемая функция ошибок, не имеющая представления в замкнутой форме. В центральной предельной теореме утверждается, что среднее η случайных переменных приближается к нормальному распределению по мере того, как η стремится к бесконечности. Такому свойству подчиняется почти любая коллекция случайных переменных, при том условии, что значение дисперсии любого конечного подмножества переменных не доминирует над значениями дисперсии других конечных подмножеств.
|