В математике сформулировано определение вектора как элемента векторного пространства, но мы будем использовать более конкретное определение: вектор — это упорядоченная последовательность значений. Например, в двухмерном пространстве могут быть определены такие векторы, как х=<3 , 4> и у=<0, 2>. В этом приложении соблюдаются обычные соглашения об обозначении в нем векторов с помощью полужирных символов, хотя некоторые авторы отмечают имена векторов с помощью стрелок или знаков надчеркивания: χ или у. Элементы вектора обозначаются с помощью подстрочных индексов:

Двумя фундаментальными операциями над векторами являются векторное сложение и скалярное умножение. Векторное сложение х+у — это поэлементная сумма: х+у=<3+0 ,4+2>=<3,6>, а скалярное умножение — это операция умножения каждого элемента на некоторую константу: 5х=<5хЗ , 5х4>=<15, 2 0>.

Длина вектора обозначается как | x | и вычисляется путем извлечения квадратного корня из суммы квадратов элементов:. Точечное произведение (называемое также скалярным произведением) двух векторов, х у, представляет собой сумму произведений соответствующих элементов; иными словами,

или в данном конкретном случае: х у=3х0+4х2 = 8.

Векторы часто интерпретируются как направленные отрезки прямых (напоминающие стрелки) в n-мерном евклидовом пространстве. В таком случае операция сложения векторов эквивалентна совмещению конца одного вектора с началом другого, а точечное произведение х-у эквивалентно выражению | x | | у | cosθ, где θ — угол между χ и у.

Матрица — это прямоугольный массив значений, упорядоченных по строкам и столбцам. Ниже показана матрица m с размерами 3x4.

Первый подстрочный индекс термаопределяет строку, а второй — столбец.

В языках программирования терм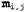часто записывается как m [ i, j ] или m [ i ] [ j ].

Сумма двух матриц определяется путем сложения соответствующих элементов, поэтому . (Если матрицы m иn имеют разные размеры, то их сумма не определена.) Можно также определить операцию умножения матрицы на скаляр: . Операция умножения матриц (получения произведения двух матриц) является более сложной. Произведение mn определено, только если m имеет размеры axb, а n — размеры bхс (т.е. вторая матрица имеет количество строк, совпадающее с количеством столбцов первой матрицы); результатом является матрица с размерами ахс. Это означает, что операция умножения матриц не коммутативна — в общем случае. Если матрицы имеют приемлемые размеры, то результат их умножения являются следующим:

Единичная матрица I имеет элементы, равные 1, если i=j, и равные 0 в противном случае. Она обладает таким свойством, что mI = m при всех т. Транспозиция матрицы m, которая записывается как, образуется путем превращения строк в столбцы и наоборот, или, более формально, путем выполнения операции