Матрицы используются для решения систем линейных уравнений с помощью процедуры, называемой алгоритмом удаления элементов Гаусса-Джордана, который характеризуется показателем. Рассмотрим следующее множество уравнений, для которого можно найти решение в терминах х, у и z: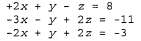

Эту систему уравнений можно представить в виде следующей матрицы: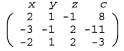

Здесь строка χ у z с не входит в состав матрицы; она служит лишь в качестве напоминания, к чему относится каждый столбец. Известно, что если обе стороны уравнения будут умножены на константу или если это уравнение будет сложено с другим уравнением, то полученное уравнение останется действительным. Метод удаления элементов Гаусса-Джордана действует по принципу повторного выполнения подобных операций таким образом, чтобы вначале была удалена первая переменная (х) из всех уравнений, кроме первого, а затем эти действия продолжались в форме удаления i-й переменной из всех уравнений, кроме i-ro, для всех i. Удалим χ из второго уравнения, умножив первое уравнение на 3/2 и сложив его со вторым. В результате будет получена следующая матрица:

Продолжая аналогичные действия, удалим х, у и z и получим следующее:

Таким образом, решением является х=2, у=3, z=-1 (проверьте это решение!).